A rendszerlogikai alapú világképben a részecskék gömbrészecskékre és tetra-részecskékre oszthatók, és nagyság szerint növekvő, periodikus sorozatot alkotnak. A gömbrészecskék közül már ismerjük a neutrínót, a protont és a neutront. Még nem fedeztük fel az ősatomot, valamint a neutrínó és a proton közötti, a mágnességért felelős elektrínót. A tetra-részecskék közül ismerjük a fotont (tetra-neutrínó), az elektront (tetra-elektrínó) és a Hélium atommagját, az Alfa részecskét. Nem fedeztük még fel a tetra-ősatomot. Ezek felfedezésének hiánya azonban nem akadályozhat meg abban, hogy a már ismerteket jobban használjuk a világunk megismerésére. Tudjuk azt, hogy a részecskék áthatoló vagy visszaverődő képessége nem egyforma, ami nem magyarázható kizárólag csak a méretükkel. A rendszerlogikai világképben a gömbrészecskék mindegyike áthatoló, míg a tetra-részecskék az anyag felszínéről visszaverődnek, és ezért arról információt képesek hozni. Azt is tudjuk, hogy képalkotásra a természet a fotont használja. Erre alapozva alakult ki az élőlények szeme. Mi is ezt használtuk az optikai eszközök fejlesztésével egyrészt a mikrovilág megismerésére és leképezésére, de távcsőként is a távoli dolgok észlelésére.
Amikor ez már nem volt elég a számunkra, akkor kezdtük el alkalmazni az elektront, mint elemi töltéshordozót az elektronikus leképezésre és képtovábbításra, valamint a mikrovilág feltárására az elektronmikroszkóppal. Mindezt úgy, hogy nem voltunk tisztában azzal, hogy egy másik, a fotonhoz hasonló tetra-részecskét használunk, és csak azért sikerülhet használni, mert tetra-részecske. Ehelyett töltéshordozónak tekintettük, és a berendezést is ehhez az elképzeléshez alakítottuk ki. Valójában minden tetra-részecskét úgy kellene használnunk, mint a természet a fotont. Az áramlása vagy sugárzása fizikai visszaverődésére kellene észlelő berendezést kifejlesztenünk. A természet nem szkennel pontról-pontra, hanem egységes képet elkot.
Elméletileg rájöhettünk volna, hogy valamilyen komoly különbségnek kell lenni a proton és az elektron között a feltételezett elektromos töltésen kívül is, mert a protonnal a leképezés, nem működik. Persze, akkor még nem tudhattuk, hogy a nagy áthatoló képességű gömbrészecskék egyike sem alkalmas a leképezésre. Arra csakis a tetra-részecskék alkalmasak, de csak akkor, ha nem töltéshordozóként használjuk őket. A természet sem ezt teszi.
A két leképezésre használt részecske (foton és elektron) tömege között az arány kb. 1:8000 a rendszerlogika szerint. A felületük között 1:400 és az átmérőjük között 1:20 az arány. Ez azt jelenti, hogy azokon a helyeken, ahol a foton az anyagon ellenállás nélkül áthatol, mert átfér az anyag szerkezetének résein, vagy a mélyére jutva elnyelődik, azaz nem verődik vissza, ott a 400-szor nagyobb felületű elektron visszaverődik és információt hoz a felületről. Ennek azonban ára van. Az elektronmikroszkóp építéséhez bonyolult technológia, nagy vákuum, sok és nagy energia, valamint másodlagos leképező berendezések voltak szükségesek. Ráadásul élő anyagot nem lehet vele vizsgálni. És még ezzel sem értük el azt a felbontóképességet, és kontrasztosságot, hogy két atommagot külön pontnak lássunk úgy, hogy még az alakjuk is kivehető legyen.
Észre kell azonban vennünk, hogy mindezt azért nem sikerült elérnünk az elektronmikroszkóppal, mert nem azt a képalkotási technikát használtuk, mint a természet. Nem vettük észre és figyelembe, hogy az optika szabályai minden tetrarészecskével való képalkotásban érvényesek! Ha nem is tudatosan teszzük, az optikában két tényezőt kombinálunk: a szórt fényt, és azt a fényt, amivel a tárgyat „levilágítjuk” (, direkt megvilágítás,vaku). A természetben ugyanígy látunk: a Nap levegőben szóródó fényével és a direkt napsugarakkal. Ahhoz, hogy kontrasztos és mélységgel rendelkező képet kapjunk, ezt a kettő mindenképpen együtt szükséges alkalmazni.
Van azonban még egy optikai ismeret, amelyet nem hagyhatunk figyelmen kívül, noha az elektronmikroszkóp megalkotásakor éppen ezt tettük. Ez pedig az a közeg, amelyben a természetben látunk, a levegő. Ennek hiányában nem kapunk éles képet. Gondoljunk csak arra, hogy a víz alatt is csak akkor látunk élesen, ha a szemünk és a víz között legalább egy kis levegőrésteg van, amit pl. egy úszószemüveg már képes biztosítani.
Most, hogy a rendszerlogika segítségével feltárult a részecskék alakja és összetétele közötti hasonlóság, megnyílt a lehetősége annak is, hogy az általunk ismert harmadik tetra-részecskét vessük be a képalkotás és a mikrovilág megismerésében.
Az elektron és a Hélium atommag átmérője, felülete és tömege között ugyanaz az arány, mint a foton és az elektron között, amelyet fentebb láttunk. A Hélium atommag felszíne tehát 400-szor nagyobb, mint az elektroné. Így olyan felszínről is kontrasztos képet eredményező módon verődik vissza, ahonnan az elektron már nem képes információt hozni. A Hélium atommag alkalmazásával a felbontó képesség ugyanannyival nőne meg, mint a fénymikroszkóp és az elektronmikroszkóp közötti felbontási arány. Végre láthatnánk az atomokat és azok valódi alakját is. Végre a gyakorlatban kiderülne az elektron szerepe – ha van egyáltalán – az atomok összekapcsolásában.
A rendszerlogika szerint a foton tömege az elektron tömegének közel 1/8000-ed része. Ezért az elektron természetes sebességének a fénysebesség 1/8000-ed részének kellene lennie. A Hélium atommag tömege 8000-szer nagyobb az elektron tömegénél, tehát a sebességének is az elektron sebességének 1/8000-ed részének kellene lennie ahhoz, hogy képalkotásra használhassuk, mint részecskét, nem pedig, mint töltéshordozót.
A rendszerlogikai elemzés azt mutatja, hogy a jelenlegi elektronmikroszkópokat is lehetne még továbbfejleszteni. Jelenleg éppen az a baj, hogy az elektronokat nem, mint tetra-részecskéket alkalmazzuk azzal a sebességgel, amely a tömegükhöz természetszerűleg tartozna a sebesség-tömeg arányból levezethetően, hanem erősen gerjesztett állapotú, túlsebességgel mozgó töltéshordozóként. Ezzel a sebességgel és energiatartalommal az elektronsugár csak roncsolja az anyagot, nem pedig visszaverődik, mint tetra-részecske, hogy egy megfelelő ernyőn nyomot hagyjon. Ezért nem vizsgálható vele az élő anyag anélkül, hogy el ne pusztítaná maga a vizsgálati módszer.
Továbbá, nincs jelen az elektron szórt „fénye” sem. Pedig mindkettő együttes alkalmazása technikailag megoldható lenne úgy, hogy még vákuum sem kell hozzá. Ebben az esetben még mágneses eltérítést sem kellene alkalmazni, hiszen van olyan optikai eszközünk (lencse), amely az elektronok esetében is alkalmazgható. Ez pedig a diafragma, amit az optikában szabályozható módon már régóta alkalmazunk.. Ráadásul ma már azt is tudjuk, hogy a méretén kívül a diafragma alakja is jelentőséggel bír a sugárzások fókuszálásában (kör, hatszög, sokszög)
Ezt a hibát nem szabad megismételnünk az Alfa mikroszkópia kifejlesztése során. Nem szabad töltéshordozónak tekintenünk, és nem szabad azzal a sebességgel használnunk a Hélium magot, amelyre az atommag bomlásából származó alfasugárzásban tesz szert. Valójában a Hélium atommag sebessége esetében a gázok áramlási sebességének, vagy a gázokban való hullámterjedés (hang) sebességének szintjéről van szó, amely nem lehet nagyobb a levegő részecskéinek a természetben előforduló maximális áramlási sebessége maximum négyszeresénél. Vagy más módon megfogalmazva: nem lehet nagyobb, mint a hangnak a terjedési sebessége tiszta Héliumgázban. A hangsebesség ugyanis az a belső határsebessége a gázoknak, amelyet a gáz saját részecskéi mozgásának sebessége nem képes önerőből meghaladni. Ez a sebesség biztosítja, hogy a képalkotásban nem jön létre torzulás a mesterséges energianövelés miatt. Az extra gerjesztés ugyanis nem csak a részecske mozgási sebességét növelné meg, hanem a perdületének és pulzációjának sebességét is, amelyek a visszaverődésben erős torzulást okoznak, és a kontrasztosságot erősen rontják. Ez a jelenség az elektronmikroszkópiában ma is fennáll, amit a gerjesztés (sebesség) csökkentésével ki lehetne küszöbölni.
Az Alfa mikroszkópia kifejlesztéséhez tehát nem kell nagy energiákat használni, és csupán olyan ernyőt (leképező eszközt) kell találni, amelyen a tárgyról visszaverődött hangsebesség alatti alfa részecskék olyan nyomot hagynak, amelyet képként képesek vagyunk láthatóvá tenni. Továbbá szükségünk van egy olyan közegre is, amely képes az alfa részecskéket szórva, szórt alfa „fényt” biztosítani.
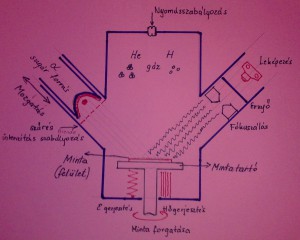
Az elméleti megfontolásoknál még egy dolgot figyelembe kell venni. Ez pedig a szabad úthossz, amely a részecskék méretének növekedésével arányosan csökken a gázközegekben. Éppen a szabad úthossz arányos csökkenése teszi lehetővé a tetra-részecskékből álló gáz-közegek alkalmazásánál (ilyen a fényközeg, az elektronközeg és a Hélium gáz is!) a nagyobb részecskékkel jobb felbontás, azaz kisebb részletek láthatóvá tételét. Továbbá úgy kell tekintenünk, mintha a minta eléréséig a leképező részecskeáram sugárzás lenne, a mintáról azonban már „hullámként verődne vissza”. az elvi elrendezés a következőképpen nézhetne ki.
Az elrendezésből látható, hogy a leképezés nem szkennelő módban történik, hanem a fénnyel való leképezés „hagyományos” módján. A morfológiai alapvetés során eddig még nem sikerült tisztázni, hogy szóró közegnek hélium vagy hidrogén gáz lenne-e jobb, ezért szerepel mindkettő, noha valójában csak az egyikkel működik a rendszer.
A morfológia modellezés rendszerlogikai alapon képes láthatóvá tenni az atommagok alakját és kapcsolódásaik módját. Ennek a kísérleti igazolására csak akkor van esély, ha a mikro-leképezésben is előrelépés következik be, amit az Alfa mikroszkópia kifejlesztésétől várunk.
Nézzük meg a következő példákon keresztül, hogy már az elektronmikroszkópia is mennyire közel került ahhoz, hogy az atomok alakját megmutassa, és azt is, hogy az milyen jól egyezik a morfológiai modellezéssel előállított formákkal.
Az első képpáron a már bemutatott nikkel atommag morfológiai modellje, és a nikkel (egyik) felszínének STR képe látható. (minden anyagnak három felszínalkotó iránya van)
A második képpár a platina atommagjának morfológiai modelljét mutatja és a platina felszínének STR képét.
Ennek a képnek a helyes értelmezéséhez tudnunk kell még valamit. Bár nem közismert, de tény, hogy a fémeket más-más irányban csiszolva más-más felületi simaságot lehet elérni. Ez a fémrács szerkezetből, és azon belül az atomok helyzetéből fakad. A morfológiai modellezés azonban azt mutatja, hogy ezt a jelenséget valójában az atomok alakja és egymáshoz való kapcsolódása hozza létre. Amikor – mint a képen is – az atomok csúcsukkal állnak egy irányba a felületen, akkor ilyen képet mutatnak. Amikor pedig lapjukkal állnak a felület felé, akkor olyat, mint a nikkel esetében láttunk. A harmadik lehetőség az, amikor az oldalélükkel fordulva állnak a csiszolási felület felé. Ez háromféle felszíni simaságot is eredményez.
Még egy dolgot meg kell jegyeznünk az atomoknak a testté kapcsolódásával kapcsolatban. Az atomok a fémrácsban nem valódi kristályszerkezetet alkotnak, hanem itt is a legszorosabban illeszkedő szerkezetet, amelyben az egyes atomi rétegekben csak annyi üres hely marad, amennyi az atomok nem összeférhető felületei meghagynak. Ez, és a szerkezeti hibák együttesen okozzák a fémek esetében a fajsúlybeli különbségeket. A legnagyobb elérhető fajsúly a világegyetemben a gömbrészecskék szoros illeszkedésével alakul ki, amelyet a földi körülmények között a tiszta irídium fém közelít meg a legjobban a maga 22,5 körüli fajsúlyával. Ez az érték már majdnem azonos a tudományban „neutronanyagnak” nevezett, legsűrűbbnek tartott anyag fajsúlyával.
Valójában, ha a gravitációt a rendszerlogika szűrőjével helyesen értelmezzük, a Föld átlagfajsúlya is eléri a 22-es értéket. A gravitációnak a tömeggel való összefüggése alapján, amely valós összefüggés, a gravitációban résztvevő teljes tömeg csak akkor van a felszínén mérhető hatás mögött, ha a távolságot nem a középpontjától, hanem a felszínének az ellentétes oldali megfelelő pontjától számítjuk. Ez a sugár távolságáról az átmérőre való növekedés a számításban azt eredményezi, hogy a kétszeres távolság négyszeres tömegnövekedést jelent. A Föld eddig számított 5.5-ös átlagfajsúlya így 22-re módosul. Ezzel válik érthetővé, hogy a magma gyakorlatilag neutronanyag sűrűségű ősanyag, amely a felszínre kerülve a hűlés és kristályosodás útján válik elemekké, és fajsúlyát az eltérő kristályszerkezeti illeszkedés csökkenti le az elemek ismert és mért fajsúlyára.
Továbbmenve a modellek és az STR képek összehasonlításában, most lássuk az arany modelljét és AFM képét. Láthatjuk, hogy alakja a platinára mennyire hasonlít.
A következő képen pedig két, eltérő irányban lapított aranyfüst lemez STR képét láthatjuk, ahol jól látható a fentebb kifejtett irányfüggő szerkezet, amit az atomok alakja okoz.
A következő képen pedig az egyik legnagyobb atommag, az Urán modelljét láthatjuk, valamint annak STR képét. A két kép önmagáért beszél. A kristályszerkezet pontosan ismétli az atom alakját.
Képzeljük el, hogy mennyivel jobban megértenénk az anyag szerkezetét, ha az Alfa mikroszkópia ennél négyszázszor jobb felbontású, és kontrasztosabb képet állítana elénk a vizsgált anyagokról. Éppen itt az ideje a módszer kifejlesztésének.


 Téma:
Téma:  Címkék:
Címkék: