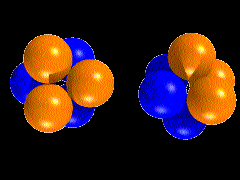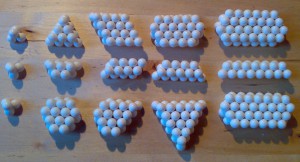Atomok és molekulák általános alaktani modellezése
Bevezetés az alaktani modellezés módszerébe
Az alaktani (morfológiai) modellezés egy olyan gyakorlati módszer, amely elérhetővé teszi a láthatatlant, és kézzel foghatóvá az elérhetetlent. Ez az állítás ellentmondásosnak hangzik, azonban igaz állítás, mert a gyakorlatban igazolható. Bárki maga megtapasztalhatta, aki valamilyen nagy test (épület) kicsinyített makettjét már elkészítette, vagy csupán látta.
A morfológiai alapú modellezés ugyanezt teszi, csak a morfológiai illeszthetőség szabályainak alkalmazásával a láthatatlanul kicsit modellezi nagyban. Ezt a módot ugyanaz teszi lehetővé, mint ami a kicsiben való modellezést. Az a tény, hogy az anyagi testek bizonyos megváltoztathatatlan tulajdonságokkal rendelkeznek. Ilyen tulajdonsága az anyagnak az, hogy a 3-dimenziós térnek egy bizonyos darabját kitölti, azaz térfogata van. A másik ilyen tulajdonsága, hogy sűrűsége van. A kettő együtt adja az anyag newtoni értelemben vett tömegét, azaz anyagmennyiségét. A harmadik, általában elhanyagolt tulajdonsága az anyagnak, hogy valamilyen formája van még akkor is, ha az pillanatnyilag nem határozható meg. A három tulajdonság együtt hozza létre a szilárd testek megtapasztalható változatlanságát és meghatározhatóságát (állandóság). Ezek közül a faktorok közül a forma az, amellyel mindenfajta modellezés operál, még ha ez elsőre nem is annyira szembetűnő.
Ahhoz, hogy valamilyen testet modellezni tudjunk, pusztán annyit kell tenni, hogy meg kell keresni azt a tényezőt, amely változatlan marad akkor is, ha a test kicsiny, és akkor is, ha a test nagy. Ezek egyike a geometriai forma, amelynek paraméterei mérhetők, és egymáshoz való viszonyuk és arányuk akkor is ugyanaz marad, ha a test nagy, de akkor is, ha mérhetetlenül kicsiny. Ezen alapul a morfológiai modellezés módszere: a léptéknövelés, vagy lépték csökkentés.
Tény és való, hogy még senki nem látott a saját szemével atomot vagy molekulát, de ez nem jelenti azt, hogy ezek ne lennének vizsgálhatók más módszerekkel, mint a fényre alapozott leképezés. A léptéknövelés módszere például jól ismert a vegyészetben, ugyanakkor a kémia az, amely szakembereinek úgy kell manipulálniuk az anyagot, hogy sem a kiinduló állapot összetevőit, sem a végállapot összetevőit nem látják. Ennek ellenére többnyire sikeresen hozzák létre a megkívánt anyagokat a megkívánt mennyiségben. Mennyivel könnyebb lenne a dolguk, ha a rendelkezésükre állna egy módszer, amely kézzelfogható, manipulálható közelségbe hozza a számukra tevékenységük tárgyait, az atomokat és a molekulákat.
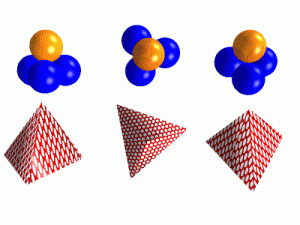
Most ahhoz hasonlóan kell dolgozniuk, mint annak, aki a horizont mögött már eltűnt hajó nyomdokvizének tulajdonságaiból akarja megállapítani a hajó méretét, formáját, sebességét, szerkezetét és felépítését, netán még a matrózok számát is. Nehéz, de nem lehetetlen feladat, még ha magában hordozza is a tévedés lehetőségét, hiszen éppen erre valók a modellkísérletek kicsiben, majd a helyesnek gondolt modell léptékének megnövelése ipari méretekre. A morfológiai modellezés egy eddig nem vizsgált, de a későbbiekben jól láthatóan döntő fontosságúnak bizonyuló tulajdonság – a térgeometriai forma – láthatóvá tételével képes ehhez segítséget nyújtani.A geometriai formák egy test esetében lehetnek egyrészt síkgeometriai formák, amelyek a test egyes felületeit alkotják, de lehetnek görbe felületek is. Ezek lehetnek szabályosak, de az ember számára szabálytalannak tűnő formák is. Ugyanez a helyzet a testek térgeometriai formájával is. A felületek határolta testek a térben is lehetnek szabályosak, és szabálytalannak tűnők. Ennek illusztrálására álljon itt példaként a platóni szabályos testek sora.
Platóni (szabályos) testek. Forrás: Tankönyvtár
 |
Noha első látásra nem szembetűnő, de a platóni szabályos testek egyike minden más szabályos testhez képest is különleges. Ez a tetraéder. Ennek a testnek ugyanis – a többivel ellentétben – nincsenek a testen belül átmenő átlói, csak élei, csúcsai és lapjai vannak. Nincsenek szemben fekvő párhuzamos lapjai sem, mint a többi testnek. Ez a tulajdonsága a későbbiek során válik jelentőssé, amikor a modellezésben a testeknek a hatásokkal szemben mutatott viselkedését vizsgáljuk, amelyet a formájuk és felületeik egymáshoz viszonyított helyzete – mint majd látni fogjuk – döntően meghatároz. Az állandóságot pedig éppen a hatásokkal szemben mutatott ellenálló képesség alapozza meg. Ha a formája megfelelő, a test hosszú ideig megőrzi állandóságát. Más esetben elkerülhetetlenül erodálódni fog. Éppen ezek miatt a tulajdonságai miatt a tetraéderforma egy alapforma szerepét fogja betölteni a modellezésben is, mint ahogyan a természetben is azt teszi.
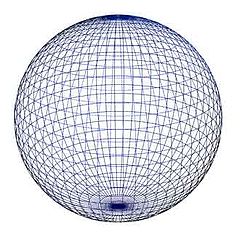
De láthatjuk azt is, hogy a szabályos testek sora hiányos. Nem szerepel benne a gömb, noha a természet számtalan esetben létrehozza, és szinte mindenütt előfordul a világunkban. Ennek valószínűleg pusztán annyi az oka, hogy nem határolják szabályos síklapok. Az alaktani modellezésnél azonban erre nem lehetünk figyelemmel, ezért a gömb is egyike lesz a morfológiai modellezés alapformáinak. Különösen azért, mert a gömb az egyetlen térgeometriai forma a szabályos testek között, amelyből homogén térbeli szerkezet alakítható ki. Továbbá: A gömb az egyetlen olyan forma, amelynek ugyan nincsenek sem síkjai, sem szögei, azonban az azonos méretű gömbökből összeállított térszerkezetnek meghatározott szögei, síkja és lapjai lesznek, amelyek szöge ráadásul mindig azonos marad! Emellett: noha a többi szabályos testtel összehasonlítva úgy tűnhet, hogy a gömb nem illeszthető szabályos forma, valójában a gömb az egyetlen tökéletesen illeszthető test, amelyből bármilyen forma létrehozható. Valójában éppen a többi szabályos test illeszthetősége hiányzik, vagy korlátozott. Sokszor még köztes, illesztő test alkalmazásával sem egyesíthetők! Ugyanakkor, ha egy platoni szabályos testet gömbökből alkotunk meg (lásd tetraéder), akkor annak az illeszthetősége azonnal megjavul. Miért is? Mert az eddigi sík felületein szinguláris, illesztő helyek jelennek meg. Lássuk tehát a gömböt e felismerések fényében.
Gömb. Forrás: Wikipédia
Noha közismert forma, mégis vegyük szemügyre alaposabban is a gömböt. Úgy, mintha most látnánk először, és gondolkodjunk el rajta, hogy mitől is mondunk gömbnek egy gömböt. Általában erre az a szokásos válasz, hogy attól gömb egy gömb, mert minden felszíni pontja egy képzeletbeli középponttól azonos távolságra van. Igen, de ha alaktani szempontból kell meghatároznunk, egy képzeletbeli középponttal semmire sem megyünk. Különösen akkor nem, ha távolságot sem tudunk mérni. Ezért a gömb alaktani szempontból attól lesz gömb, mert a felületének görbülete bármely két pontja között azonos. Ez az, ami első látásra, mindenki számára észlelhető (érzékelhető), és ezért nyilvánvaló. Ezzel ugyan látszólag nem mondtunk semmit, de csak látszólag. Valójában azt mondtuk ki, hogy a gömb egy olyan test, amelynek a felületén egyetlen kitüntetett (szinguláris, más pontoktól bármiben is eltérő) pontja sincs.
Ezzel el is értünk az alaktani modellezés első sarokkövéhez, az illeszthetőséghez. Mi az illeszthetőség? Az illeszthetőség morfológiai szempontból a síklapokkal határolt testeknek az a tulajdonsága, hogy nagy felületen képesek egymáshoz tapadni, ha az alakjuk megfelelő. A gömb esetében, amelynek nincsenek sík lapjai, belátható, hogy bármilyen módon próbálunk is illeszteni két gömböt, mindig csak egyetlen ponton fognak egymáshoz érni. Illeszthetőség nélkül a szilárd testek semmilyen valóságnak megfelelő térbeli modellezése nem képzelhető el. Legalábbis a valóságot helyesen tükröző modellek nem alkothatók. Az illeszthetőség összefüggései ezért a morfológiai modellezés alapját alkotják.
A gömbre, mint alaktani szempontból szabályos testre még egy különleges tulajdonsága miatt vissza kell térnünk. Noha nem csak a gömbre, de minden más testre is igaz, mégis a gömbnél van a legnagyobb jelentősége annak, hogy a test, amit a felület határol tömör, vagy üreges-e. Azért, mert a gömb egy másik gömbbel, vagy bármely síklapokkal határolt testtel csak egyetlen pontban illeszthető, tehát nem lesz közömbös, hogy az egyetlen ponton ható összetartó erőnek egy tömör, ezért nagy tömegű, vagy egy üreges, ezért kis tömegű testet kell megtartania. Emiatt – hogy a valóságot helyesen tudjuk modellezni – az alaktani modellezésben megkülönböztetünk tömör testeket és héjtesteket. A héjtestek az alaktani modellezés szempontjából olyan felületek által határolt testek, amelyek üres teret zárnak közre.
Ábra: gömbhéj és tömör gömbtest keresztmetszete.
Az ábráról láthatjuk, hogy a tömör test kétdimenziós leképezése a kör, míg a héjtesté egy gyűrű. Ez még akkor is így van, ha a felületnek semmilyen vastagságot nem tulajdonítunk. Ezért a továbbiakban a színezett belsejű kör egy gömbtest keresztmetszetét, a belsején színezetlenül hagyott kör pedig egy héjtest keresztmetszetét fogja jelenteni.
Az illeszthetőség egyik legfontosabb faktora a felület. A felület is közismertnek tűnő fogalom, de valójában nem az. Általában nem gondolunk rá, hogy egy felület egyben határ is. Elhatárolja a testet a környezetétől. Ezért a morfológiai modellezésben a felületet határfelületnek nevezzük. Az sem szembetűnő, hogy közeg is. Minden, a testet kívülről érő hatást a határfelület közvetít a test anyaga irányába, vagy nem közvetíti, ami a határfelület másik lényeges tulajdonsága. A határfelület a testek illesztésében is ilyen kettős szerepet játszik: lehetővé teszi az illeszkedést, vagy nem teszi azt lehetővé. Ezek a tulajdonságai egzakt módon meghatározhatók.
A határfelület alakján kívül a milyensége (a felület simasága és egyenletessége) szintén döntő szerepet játszik az illeszkedés létrejöttében. Általában belátható, hogy minél nagyobb felületen érintkezik (és illeszkedik is) két test, annál erősebben képes egy ugyanakkora összetartó erő a két testet egyesíteni. Annál nagyobb erő kell a két test szétválasztásához. Ez is mindennapi gyakorlati tapasztalat.
A simaság viszont relatív fogalom, amelyet a modellezés szempontjából is meg kell valahogyan határozni. Mivel minden anyagi test kisebb részekből, és azok is még kisebb részekből tevődnek össze, anélkül, hogy ezeket pontosan ismernénk, addig folytathatjuk a sort, amíg a már nem mérhető nagyságú pontokig el nem érünk. A morfológiai modellezés ezért a felületeket az érintkező pontok számával helyettesíti, amikor egy kapcsolódás erősségét kell meghatározni.
A határfelületek érintkezésének nagysága, és ezzel az összetartó erő relatív nagysága is meghatározható azoknak a pontoknak a számával, amelyek fizikailag egymáshoz érnek. Ez különösen fontos tényező, mert az atomi és molekuláris méretekben tökéletesen sima felületekkel nem számolhatunk. Ezért célszerűbb ezek helyett érintkezési pontokkal számolni. Ezek száma, és az érintkező testek tömege alapján nagy bizonyossággal eldönthető, hogy egy adott módon illeszkedő testek együtt fognak-e maradni, azaz a modell a szilárd testekre jellemző állandóságot helyesen képezi-e le.
Az érintkező felület nagysága (pontok száma) viszont függ a felület alakjától. Síkfelületek esetén a teljes felülettel (az összes ponttal) lehetne számolni. Ez azonban egy olyan ideális eset, amely rendkívül ritkán fordul elő, hiszen a síkfelület maga is ritka madár a természetben. Ennél sokkal gyakoribb a görbe felületek érintkezése, amely az ideálisnál sokkal kevesebb ponton jön létre, és a testek alakjától sokkal erősebben függ, mint a síkok esetében. Ezért a morfológiai modellezésben a testek egyszerre lehetnek makro-nézetben síklapokkal határolt testek, és mikro-nézetben (felületen) görbe felületekkel határolt testek. Ezt nézzük meg a gyakorlatban is.
Ábra: gömbökből összerakott egyenlő oldalú, háromszög alapú piramis (tetraéder)
Az ábrán jól látható, hogy a test ugyan (csúcsain csonka) tetraédert formáz, amelynek felületei makro-nézetben síklapok, de az illeszthetőség szempontjából – mikro-nézetben – nem azok, hanem gömbökből álló „durva” felületek. Két ilyen tetraédert nem tudunk úgy illeszteni, mint két síklapokkal határolt tetraédert. A durva felületek részben egymásba csúsznak, és ezért a lapok oldalirányban is elmozdulnak, amíg el nem érik a legszorosabb illeszkedés állapotát az aktuálisan ható erőknek megfelelően.
Ezzel el is érkeztünk a morfológiai modellezés második sarokkövéhez, a térnek azokhoz a tulajdonságaihoz, amelyek között a modellezni kívánt testek egymáshoz kapcsolódni fognak a térben. A tér morfológiai szempontból az, amelynek egy részét a modellezett test a térfogatával kitölt. A térnek, amelyet morfológiai szempontból alapvetően üresnek (anyagmentesnek) tekintünk, mégis vannak tulajdonságai. Morfológiai szempontból kétféle teret különböztetünk meg: az irányított és az irányítatlan teret.
Nézzük meg, hogy mit is érthetünk térirányításon a gyakorlatban. Mivel a morfológiai modellezés során a valóságot valósághűen kell modelleznünk, ezért a valóságban létező hatásokat is figyelembe kell vennünk, mert azok befolyásolják a morfológiai illeszthetőséget. Mit is kell ez alatt érteni?
Az ismert világunkban minden testre hatások hatnak. Ezek egyike a gravitáció, amely minden testre, ugyan eltérő mértékben, de hat. Egy másik ilyen hatás a mágnesség, amely a testeket morfológiai szempontból két csoportra osztja: olyan testekre, amelyekre hat, és olyanokra, amelyekre a ferromágnességtől eltérő módon hat, vagy egyáltalán nem hat. Hasonló hatás az elektromos töltés is, amely szintén két csoportra osztja a morfológia szempontjából az anyagi testeket. Olyan testekre, amelyek között távoltartó erőként, és olyanokra, amelyek között közelítő erőként hat. Összefoglalva, az ilyen típusú hatásokkal rendelkező tereket nevezzük a morfológiában irányított tereknek. A morfológiában annak nincs jelentősége, hogy ezek a térirányító hatások a térnek mekkora darabjára terjednek ki, milyen erősségűek és mekkora a hatótávolságuk. Pusztán a létük érdekes, mert a testek létrejöttében, vagy létre nem jöttében szerepet játszanak. A modelljeinket alapesetben mindig gravitációsan irányított térben hozzuk létre, ezért a térirányításnak ezt – a földfelszínen, a modellezés helyén, egyirányú – fajtáját mindig számításba vesszük.
Nézzünk erre egy példát. A földi viszonyok között a határolt víz felülete mindig merőleges a gravitáció irányára. Ezt nevezzük vízszintesnek, amely azért kaphatott önálló nevet, mert mindenütt megbízhatóan állandó jellemző, amelyhez viszonyítani lehet más testek helyzetét. Ugyanez a víz egy súlytalanságban levő űrhajó kabinjában nem igazán határolható, mert szabadon lebegve, határolatlanul mindig gömb alakot vesz fel. A morfológiai modellezés szempontjából erre mondjuk azt, hogy az a hatás, amely a Földön a vizet vízszintes felületűvé alakítja, a súlytalanságban nem működik, tehát a tér az előbbi esetben irányított, az utóbbiban pedig irányítatlan morfológiai szempontból. Helyesebben: minden irányból irányított, ami morfológiai szempontból ugyanazt eredményezi. Az utóbbi esetben ugyanis fennáll annak is a lehetősége, hogy a tér minden irányból egyenletesen irányított, amit a morfológiai modellezésben nem is zárunk ki, sőt, esetenként számítunk is rá, de főként akkor, amikor az összetartó erőkről van szó. Az illeszthetőség szempontjából a morfológiai modellezésben az abszolút irányítatlan tér és a minden irányból egyenletesen irányított tér tehát egyenértékű.
A morfológiai modellezés szempontjából – munkahipotézisként – mindent, ami anyagból épül fel, testek halmazának tekintünk. Legyen az a legkisebb, akár még nem is észlelt részecske, morfológiai szempontból az is test, amely maga is formával, térfogattal és sűrűséggel rendelkező kisebb testek halmaza. A morfológiai modellezésben ez alól egyetlen kivétel van: a démokritoszi értelemben vett oszthatatlan atom, amelyet az értelemzavar kiküszöbölése érdekében (hiszen az atom kifejezés egy oszthatónak bizonyult testre már foglalt) a morfológiában ősatomnak nevezünk. Az ősatomot a morfológiai modellezésben mérhető kiterjedés nélküli gömbnek tekintjük.
Ezzel érkeztünk el a morfológiai modellezés harmadik sarokkövéhez, amely több összefüggő hipotetikus, ám a gyakorlatban bizonyítható állításból tevődik össze. Ezek az állítások szorosan kapcsolódnak a léptéknöveléshez is, amely a modellezés alapvető módszere. Egyúttal egy teljes formai világ, egy valódi rendszer kapuját is megnyitják a vizsgálódó elme számára. Ezek az állítások a következők: Ha az anyagot felépítő részecskék valamelyikének a formáját gömbnek posztuláljuk, akkor alaktani értelemben elkerülhetetlenül bekövetkezik az a helyzet, amely a következő állításban fogalmazható meg: Azonos méretű gömbökből egy nagyobb méretű tökéletes gömböt csak akkor lehet előállítani, ha a gömbök száma egy bizonyos nagyságrendet elér. (A gömb alatt itt nem a gömböt nagyjából megközelítő formákat értjük, hanem a gömb morfológiai meghatározásának megfelelő felületet.) Ez a nagyságrend pontosan meghatározható. A nagyságrendek közötti számszerűsíthető összefüggés minden egymás után következő nagyságrendre igaz.
Másként megfogalmazva: Amennyiben az anyagot felépítő részecskék bármelyikét, bármely nagyságrenden gömbnek képzeljük el, akkor tudomásul kell vennünk, hogy a gömbök illeszthetőségének természetes összefüggéseiből fakadóan csakis kötött módon alkothatunk ezekből a részecskékből testeket. A testek egy nagyságrenden belül való modellezésének felső határa az a részecskeszám, amelyből újra gömb keletkezik. Ekkor a sorozat, a következő nagyságrendben újra kezdődik a megelőző nagyságrend felső határát jelentő gömbrészecskével. A morfológiai modellezés éppen ezzel foglalkozik. Ugyanis abból a felismerésből indul ki, hogy az anyagot felépítő részecskék közül több is gömb formájú, és ezek a részecskék a formavilág egy-egy nagyságrendjének kiinduló részecskéi.
A morfológiai modellezés szempontjából gömbnek tekintjük a passzív ősatomot, a passzív neutrínót, a passzív elektrínót és a passzív neutront, valamint ezek hatóképes párjait. Hatóképesnek a morfológiai modellezés azt a részecskét tekinti, amely valamely térirányító erőt használ a más részecskékhez való kapcsolódáshoz. Passzívnak azt a részecskét tekintjük, amelyik a kapcsolódáshoz összekötő erővel nem járul hozzá. Az atomi és molekuláris morfológiai modellezésben ezek közül a proton-neutron hatóképes-passzív párost fogjuk használni, amelyeket az anyagfelépülés negyedik periódusa kezdő részecskéinek tekintünk.
(Az elektrínó a morfológiában alkalmazott neve az elektronnak megfelelő részecske egynegyedét kitevő, gömb alakú, hatóképes és passziv változatban is létező, jelenleg még hipotetikus részecskének.)
Láthatjuk, hogy a morfológiai modellezés az anyagot felépítő részecskéket periodikusan ismétlődő sorozatban képzeli el, amelynek első tagja mindig gömb. Meg kell még említeni, hogy a sorozat második, valódi részecske tagjának a modellezésben a négy gömbből előállított tetraéder formájú részecskét tekintjük, amely a további modellezés önálló építőköve is egyben. Ezt a részecskét a morfológiai modellezésben tetra-részecskének nevezzük.
Ábra: négy gömbből álló tetra-részecske több nézetben
A morfológiai modellezés az anyag önálló építőkövének a következő alakú, összetételű és szerkezetű részecskéket tekinti.
Ábra: hatóképes és passzív gömbpárok, gömb síkhármasok, tetra-részecske, valamint a csonka tetraéder alapot formázó részecske.
Az ábrán utolsóként szereplő részecske a modellezésben panel/modul szerepet fog betölteni, amelynek létrejöttéhez a későbbiek során, a modellezés folyamatában fogunk eljutni. Ez a részecske a különleges, és rendkívüli formagazdagságot lehetővé tevő formájával külön kifejtést igényel a maga helyén.
A morfológiai modellezés célja
A morfológiai modellezés célja többes. Általában a megismerést szolgálja, mert célja a természet által az anyag felépítésében használt formáknak, valamint a formákból fakadó illeszkedési és kapcsolódási lehetőségeknek a feltárása az anyag láthatatlan méreteinek szintjén, modellezés útján.
Célja továbbá a természeti folyamatok lezajlása morfológiai feltételeinek feltárása, és modellezéssel láthatóvá tétele.
Az izotópok és molekulák morfológiai alapú modellezése során célja az is, hogy segítséget nyújtson az anyag viselkedési formáinak feltárásához, az anyag alapvető alkotórészei valóságos alakjának, a kapcsolódások módjának, és az ezekből fakadó elsődleges következményeknek a bemutatásával. Célja továbbá, hogy segítse az anyag és anyagszerkezeti tervezést a valóságnak megfelelő modellek előállításával (a nem valós modellek kiszűrésével).
A morfológiai modellezés alapvető összefüggései
A morfológiai modellezés nem elszigetelt, önmagáért való módszer, hanem az anyag felépülésével foglalkozó minden szakterület vonatkozó összefüggéseit felhasználó komplex módszer. A morfológiai modellezésben ezért nem alkalmazunk szabályokat, csak elemi (statikai, geometriai, mechanikai, energetikai, stb.) összefüggéseket. Ilyen összefüggések például:
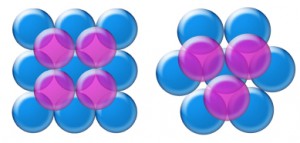
1. Egy gömbökből álló struktúra, irányított térben mindig a legszorosabban (a legtöbb ponton) illeszkedő szerkezetet veszi fel. Ez az összefüggés zárja ki, hogy a modellező statikailag és energetikailag nem valós szerkezeteket hozzon létre.
Ábra: legszorosabban illeszkedő egy- és kétrétegű szerkezet (valós)
és a nem valós illeszkedésű, többrétegű szerkezetek
Itt – anélkül, hogy elébe vágnánk a logikai összefüggés sornak – meg kell jegyeznünk néhány, a morfológián kívül eső, de a modellezésre kiható körülményt. Amikor azt állítottuk, hogy bizonyos szerkezetek nem valósak, akkor azt arra alapoztuk, hogy a testeket összetartó három számításba jöhető „erő” (gravitáció, mágnesség és elektromos tér) hatásában eltér egymástól. A gravitáció mindenkor a test tömegközéppontja felé irányuló erőként hat, ezért is lehet alapvető rendező erő. A statikus elektromos tér ehhez nagyon hasonló módon hat, mert nincsenek kitüntetett irányai, mint a mágnesnek. A sorból így a mágnesség kilóg, amely egyetlen meghatározott irányt jelöl ki két mágneses test összekapcsolódására. A legalsó ábra baloldali tagja ezt az esetet modellezi. Ha azonban csak az egyik test aktívan ferromágneses, a másik pedig passzívan, akkor a mágneses „kötés” is ugyanolyan szorosan illeszkedő szerkezetet hoz létre, mint a gravitációs vagy az elektromos erőtér. Ezért nem lehet valós az említett modell. Ahhoz ugyanis, hogy az ilyen modellt tekintsük általánosnak, azt kellene (alap nélkül) feltételeznünk, hogy minden részecske aktív ferromágneses tulajdonsággal rendelkezik. Ez pedig nyilvánvalóan nincs és nem is lehet így. Gyakorlati tapasztalat, hogy csak bizonyos részecskéket (alfa, elektron, foton) képes eltéríteni az erős mágneses tér, de nem akkor sem azért, mert aktív mágnesek, hanem azért, mert passzívan reagálnak (mint az ötvözetlen vas) a mágneses térirányításra. Ezért tartottuk indokoltnak a legszorosabban illeszkedő szerkezetet tekinteni a modellezés helyes módjának.
2. Külső hatásra az építőkövek és a szerkezet elmozdulásának iránya a mindenkori térirányítástól függő legkisebb ellenállás iránya.
3. A hatóképesség csökkenés összefüggése. Azt mutatja meg, hogy egy hatóképes építőkő hány nem hatóképes építőkövet képes megtartani. A hatóképességi szám azt mutatja meg, hogy egy hatóképes összetevő hány nem hatóképes összetevőből álló alakzatot képes megtartani. Hatóképességi optimum: az a szám, amely megmutatja, hogy egy szerkezetben milyen a hatóképes és a nem hatóképes összetevők aránya úgy, hogy a kapcsolódási erő a lehető legnagyobb, és a külső hatásoknak a forma a lehető legjobban ellenálló legyen. (Valójában a gerjeszthetőséget mutatja meg. Hasonló az anyagszerkezet felbontáshoz szükséges energiaigény értékéhez.)
4. A kötéserősség és a tömeg arányának összefüggése. Ez az összefüggés a léptéknövelés módszerének elengedhetetlen velejárója. Megmutatja, hogy a kapcsolódások során létrejövő kötések erőssége nem abszolút, hanem mindig függ a kapcsolt tömegek tömegétől, és a tömegek alakjától is, mert az határozza meg az erőkar hosszát, amelyen egy külső hatás hatni képes az összetartó erő ellenében. Másként megfogalmazva: egy egységnyi, egy ponton ható erő értéke folyamatosan csökken, ahogyan az általa összekapcsolt tömegek növekszenek, és ahogyan azok súlypontja távolodik a kötés helyétől.
5. Kapcsolódásra alkalmas hely (szinguláris hely), vagy felület hiányában két test nem kapcsolódhat össze. Ennek az összefüggésnek az alkalmazásával zárja ki a morfológiai modellezés, hogy a modellezőt a képzelete, a szépérzéke, vagy a szimmetria iránti vágya vezérelje a struktúrák létrehozásában ahelyett, hogy a valóságot próbálná leképezni.
6. A formakötöttség összefüggése. Egy adott környezeti körülmények között létrejött forma a későbbi kapcsolódásokban csakis akkor változhat meg, ha a környezeti körülmények is úgy változnak meg, hogy alkalmasak a korábbi forma felbontására és átrendezésére. Ilyen körülmények hiányában az anyag megtartja az eredeti formáját. Egy forma a modellben tehát csak akkor változtatható meg, ha a külső körülményekben az érintett szakterület eredményei szerint ilyen változás következett be, vagy az alappal feltételezhető. Ekkor is csak olyan formai átalakulás modellezhető, amelyeket az új körülmények lehetővé tesznek. Ehhez viszont alapvetően külső energia bevitelét kell feltételezni, amelynek nagysága és iránya olyan, hogy a formát képes felbontani.
7. A formai kiegészülés összefüggése. A morfológiai modellezés alap építőkövekkel dolgozik. Kisebb építőkő nem alkalmazható egy nagyobb helyett annak érdekében, hogy egy elképzelt formát alakítsunk ki. A legnagyobb lehetséges építőkővel kell mindaddig modellezni, amíg ki nem zárható, hogy az így létrejött forma fedi a valóságot. Csakis ekkor szabad kisebb építőkövekkel helyettesíteni a nagyobbat. Ezzel a módszerrel elérhető, hogy a modellezés gyakorlati tapasztalatai szerint a formák a legnagyobb építőkövekből kialakuló csonka formák egyre növekvő sorozata vezessen el a tökéletes formáig. A morfológiai modellezés tapasztalati ténye ugyanis, hogy a szabályos formák csonka változatai önálló entitások a természetben.
8. A formaváltás összefüggése. A sorozatok modellezésének tapasztalati összefüggése, amely szerint az építőelemekből összeálló tökéletes forma elérését követően a sorozatban spontán formaváltás következik be, amely új forma ugyanazokból az építőelemekből, és ugyanannyi számú építőelemből maradéktalanul kirakható, csupán az építőelemek aránya, és egymáshoz viszonyított helyzete változik meg egy kissé.
9. A szerkezeti és a formai allotrópia összefüggése. Mivel a morfológiai modellezésben minden építőelem aktív és passzív összetevőkből épül fel, ezért a nagyobb építőelemekben és a belőlük összeállított modellekben az aktív és passzív elemek eloszlása változó lehet. Ezeket az azonos formájú változatokat szerkezeti allotrópoknak nevezzük a morfológiai modellezésben. A formaváltás összefüggésénél említett azonos elemekből álló formákat pedig formai allotrópoknak, amelyeknek maguknak is lehetnek még szerkezeti allotrópjai.
Példa: tegyük fel, hogy azonos számú, két különböző színű téglából építünk egy kerti lakot és egy nagy kemencét. Nyilvánvaló, hogy a formájuk és a funkciójuk is különböző. Ezek egymásnak formai és szerkezeti allotrópjai is. Szétszedve a kemencét, abból az építőelemek más belső elrendezésével egy, a másiktól csak szín-összeállításában eltérő, de ugyanolyan formájú kerti lakot építhetünk. A két kerti lak ekkor csupán szerkezeti allotrópja lesz egymásnak. De egyikből a másikat is létrehozhatjuk. Azt azonban nem várhatjuk el, hogy egy ugyanilyen elemekből álló ház bontása során, amikor arra a szintre elérünk, hogy a beépített építőelemek száma és aránya pontosan megfelel a kerti lak, vagy a kemence építőelem számának és arányának, a bontott ház ettől kerti lakká, vagy kemencévé fog átalakulni. Ez az eset nem fordul elő a valóságban, még kis méretek esetén sem.
10. A szilárd egytest összefüggése. A morfológiai modellezésben alapvetően szilárd testeket modellezünk, noha nem kizárt a szerkezeti modellezésben a folyadékok, vagy rugalmas testek modellezése sem. Ennek okán a modellezés végtermékeként létrejött alakzatokat egytesteknek nevezzük, és a továbbiakban egytestként is kezeljük, azaz a modellezés további önálló építőköveivé válnak. (pl. molekulacsoportok modellezése során) Ekkor már csak egyes szakterületeken végzett modellezés során vagyunk figyelemmel az összetevőiknek a testen belül elfoglalt helyzetére.
11. A formafejlődés irányai és a formaváltás összefüggése. A formafejlődés nem ad hoc módon folyik, hanem mindig egy síkban vagy térben tökéletes, szorosan illeszkedő forma irányában. Ennek elérését követően az addigi kiegészülés lehetősége és az illeszkedés teljesen megszűnik. Ekkor formaváltásnak kell bekövetkeznie, amely nagyságbeli ismétlődése a korábbi formafejlődésnek. Ugyanazok a formák és köztes formák újra és újra létrejönnek a következő nagyságrendeken. A formafejlődési irányok egymásba átmehetnek. Ugyanaz a forma több irányból is létrehozható.
Példaként nézzük meg a következő ábrákat.
Ez az ábra egy formának nagyságrend szerinti megismétlődését mutatja.
Ez az ábra a formáknak egymásba való átalkulását illusztrálja.
A következő két képen formaváltások és önálló csonka formák láthatók.
Ez a kép pedig a formaváltás eredményét mutatja meg.
Vegyük észre, hogy mindegyik forma a többinek valamilyen csonka változataként is értelmezhető, mert ugyanazon építőkövek hozzáillesztésével egy másik formává alakulnak át.
12. Kapcsolódási helyek összefüggése. Egy részecske egyik oldalának egész felülete csak akkor tekinthető kapcsolódási helynek, ha egésze illeszkedik és képes kapcsolódni egy másik részecske hasonló egész felületéhez. A felület egy szeletét nem szabad ad-hoc kapcsolódási helynek kijelölni!
A kapcsolódási lehetőségek a morfológiai modellezésben
Kapcsolódási típusok:
1) egygömbös – egygömbös, azaz szabadon elmozduló kötés,
2) egygömbös – háromgömbös, azaz korlátozottan elmozduló „gömbcsukló” kötés,
3) a háromgömbös – háromgömbös, azaz kis lapkötés,
4) a háromgömbös – ötgömbös, azaz nagy lapkötés,
5) a négygömbös – négygömbös, azaz négyes kötés,
6) lapfelületi kötés.
A kötések mindegyike lehet kisebb részecskékkel megtámasztott, és térirányítással megerősített.
A kapcsolódások relatív erőssége a morfológiai modellezésben
A morfológiai modellezésben abszolút kötéserősségeket nem ismerünk, és ilyennel nem számolunk. Mivel azonban kétfajta – aktív és passzív – építőkő részecskével dolgozunk, és ezek mindenfajta kapcsolódásaival, ezért a különböző kötések erősségét egymáshoz való arányukban mégis figyelembe kell vennünk a modell stabilitásának vizsgálatakor. Ennek érdekében az aktív-aktív részecskék közötti kötés erősségét egynek (1) vesszük. Az aktív-passzív részecskekötés erősségét félnek (1/2), a passzív-passzív kötés erősségét egy negyednek (1/4) vesszük, és a felület minden kapcsolódási pontjára ezzel az értékkel számítjuk.
Az alkalmazott morfológiai modellezés módszertani elvei
A morfológiai modellezésben a modellt mindig egyeztetni kell a tapasztalattal, a természetben létezővel. Az előállított modellvariációk közül a formailag valósat, de gyakorlatilag nem valósat ki kell választani és ki kell zárni. Ugyanis a morfológiai modellezés mindig kétféle valóságot kezel. A valóságos valóságosat és a modell szerinti valóságosat. Létezik egy harmadik valóság is, a körülmények szerint valós is, amely létezhet, de pl. nem a földi viszonyok között. Az ilyen modellek alkalmasak az adott formájú és összetételű részecskék keletkezési körülményeire való visszakövetkeztetésre.
Mivel a morfológiai modellezés nem elméleti módszer, hanem gyakorlati, és az összefüggések (szabályok) felismerése a modellezés során történik, előfordulhat, hogy újabb összefüggések bukkannak fel, amelyeket fel kell venni a szem előtt tartandók közé. Vezérfonalként állítható a modellezők elé, hogy a morfológiailag valós lehet nem valóságos is, de a valóságosnak morfológiailag is valósnak kell lennie.
Például: Ha felismertük azt, hogy a természetben az anyag bizonyos tökéletes formák kialakítására törekszik, amely nem más, mint követése a természeti összefüggéseknek, akkor már morfológiai módszertani összefüggés alkotható arra, hogy pl. felépüléssel vagy elvonással is képezhetjük a természetben valósnak bizonyult formát. De ez nem jelenti azt, hogy a természet is ezen a módon állítja elő, csak azt, hogy a végállapot azonos lesz!
A felépülés módja is modellezhető, de abból vissza kell következtetni előbb a szükséges környezeti körülményekre, és kizárni vagy igazolni a mód lehetséges vagy lehetetlen voltát az adott helyen, vagy más helyen, ahol a körülmények is mások.
A modellezés során mindig kettős összefüggés-rendszernek kell megfelelni. A morfológiának és annak a szakterületnek az összefüggéseit kell együtt alkalmazni, amelyben a modellezést módszerként alkalmazzuk, mert a természetben is együtt érvényesülnek. Ha bármelyik kizárja az adott forma vagy kapcsolódás, szerkezet létrejöttét, a modellünk nem lesz valós, csak morfológiailag, bármennyire tetszetős, szimmetrikus, szép is a kialakult alakzat.
A valóságos modell felismerése: az a modell (makett), amelyről nem olvashatók le a modellezni kívánt dolog valós fizikai-kémiai tulajdonságai, nem lehet valós modell.
A morfológiai modellezésben a nem valós formák és szerkezetek kizárása több módon, a más tudományok mérhető eredményeivel való egyeztetés folyamatában, több lépcsőben zajlik. Pl. egy spirális A-P elrendezésű atom kizárható a mágneses típusú összetartó erők hajlítás-tűrési szögének megmérése alapján. Egy négy csúcsán csonka tetraéder alakú változat mellől a lapos tetraéder-alap formájú változat a kiegészüléssel tökéletessé alakulás lehetősége, vagy annak hiánya alapján kizárható. A 3+1 és 3+2 szerkezet mellől a 4+1 és 4+2 szerkezetek a statikai összefüggések alapján zárhatók ki.
Milyen külső tényezőkre kell figyelemmel lennie a modellezésnek, ha a természetet hűen akarja tükrözni? A modellezett részecskék stabilitását mindazok a gerjesztésként értelmezhető tényezők befolyásolják, amelyek a természetben előfordulnak. Tehát figyelemmel kell lennünk a hőmérsékletre, amit a morfológiában egy tágabb fogalommal, a gerjesztéssel helyettesítünk, amely mindenfajta ütközéseken alapuló, és szerkezetet felbontani képes hatást magában foglal. Olyan modell tehát nem lehet valós és stabil, amely a saját súlya alatt összeomlik, de az sem, amely gyenge behatásra bomlik fel.
Figyelemmel kell még lennünk a gerjesztő hatásokkal ellentétes összetartó hatásokra is, amelyek lehetnek a térirányítás egyes összetevői is, amelyek eredendően bontó hatások, de lehet a nyomás is, amely a morfológiában csak a zárt terek esetében tekintünk létezőnek. A nyílt téri nyomásokat a morfológiában az áramlások helyettesítik. A teret, a modell környezetében a teret kitöltő anyagot a morfológia csak közegekként értelmezi, amelyben helyileg a nyomás létrejöhet.
A morfológiai modellezésben elsősorban a természet által már létrehozott formákat keressük. Azokat, amelyek megfelelnek az ismert részecskék fizikai és kémiai tulajdonságainak.


 Téma:
Téma:  Címkék:
Címkék: