Ebben, és az ezt követő írásokban tovább folytatjuk a mágnesség kevésbé, vagy még egyáltalán nem ismert jelenségeinek tárgyalását. Ennek során eljutunk oda, hogy felismerjük: a mágnesség sem önálló jelenség. Felismerjük azt is, hogy az elektromágnesség mégiscsak létezik, de a kifejezés csak azt a jelenségcsoportot takarja, amikor a mágnesség elektromos jelenségeket generál. A mágnes-elektromosság kifejezés pedig arra a jelenségcsoportra alkalmazható, amelyet az elektromos áram keltette mágnesség hoz létre az elektromossággal való kölcsönhatásai során. Végül eljutunk arra a felismerésre, hogy mind a mágneses, mind az elektromos jelenségeket is a gravitációt létrehozó áthatoló közegek és a különböző fázisállapotú sűrű anyag kölcsönhatásai hozzák létre mindenütt a világon. Ezért nem lehet őket önálló jelenségekként, elkülönítve, vagy egyetlen jelenségcsoportként, összevontan helyesen értelmezni. A rendszerlogikának ez a komplex megközelítése mutatja meg, hogy a dinamikus világegyetem minden jelensége egyetlen és oszthatatlan rendszer része.Elsőként térjünk vissza egy kicsit a mágneses tér alakjához, mert jóval több van mögötte, mint ami első látásra észrevehető. Ehhez idézzük fel itt is azt a videót, amelyet a félreértett szupravezetésnél láttunk, ugyanis újra megnézve, még egy nagyon fontos felismerésre juthatunk. Nevezetesen arra, hogy a mágnesesen aktív testet a mágneses terénél fogva el lehet mozdítani anélkül is, hogy mechanikai módon a két test össze lenne kapcsolódva. És ez a bolygóméretű mágneses testekre, tehát a Földre is igaz!
Itt látható: http://www.molnárlászló.eu/moodle/mod/page/view.php?id=7
Ez a dolog triviálisnak tűnhet, hiszen jól ismert, hogy a mágnessel a vas tárgyakat fel lehet emelni, de az is, hogy két mágnes távolból is vonzza, vagy taszítja egymást, ezzel szintén elmozdulást hozva létre. A lényeg azonban itt egy kicsit más. Itt egy távolságtartó kapcsolat jött létre a két test között fizikai érintkezés nélkül, és az egyik test elmozdulása a másik test ugyanolyan elmozdulását vonja magával. Tehát egy olyan kötött rendszer keletkezett, amilyen más esetben csak fizikai érintkezés során jön létre. Ennek a későbbiekben még nagy jelentősége lesz, azért hívjuk itt fel rá a figyelmet. A mágneses tér alakja itt ugyanis más, mint bármely más esetben.
Visszatérve a tér alakjának közvetlen vizsgálatához, bemutatunk két módszert arra, hogy hogyan ellenőrizhető le, hogy a fólia által a tér alakjáról mutatott 2D kép megfelel-e a valóságnak.
Az egyik ilyen, egy kifejezetten a mágneses pólusok azonosítására szolgáló kis eszköz, amely egy közepén tengelyezett kis mágnest tartalmaz kétirányú elmozdulást lehetővé tevő tengelyezett keretekbe foglalva.
Ezzel az eszközzel azonban a mágneses tér hatásának távolsága és a tér alakja is jól letapogatható, azaz térbeli kiterjedése minden irányban láthatóvá tehető. Amikor az eszközt egy mágnes felszínéhez közelítjük, a kis ellenállású tengelyezett mágnes az elmozdulásával hűen jelzi az erővonalak alkotta azon határt, ameddig az adott mágnes tere kiterjed, helyesebben ameddig egy másik aktív mágnesre, vagy egy passzív ferromágnesre hatóképes.
Egy ilyen kísérlet elvégzése képes megmutatni (személyes megtapasztalás útján), hogy a mágneses tér nem végtelen, nincs mindenütt jelen, hanem csak a sűrű anyagú mágneses testek körül, és csak akkora távolságba hat el, amely arányos a test méretével és a térerősséggel. Ez azért lényeges szempont, mert implicite az következik belőle, hogy ott, ahol nincsenek égitestek (sűrű anyagú, potenciálisan mágneses szilárd testek) a világtérben, mágneses tér sem lehet jelen. Az elektrinó-közeg természetesen ettől még jelen lehet, de ha nem áramlik, vagy nincs, ami fókuszálja, a mágnesség jelensége nem jön létre belőle és benne!
Az eddigiekből máris levonhatjuk azt a következtetést, hogy a mágnesség ugyan távolhatásra képes, de ez a távolság csak a mágneses test közvetlen környezetére korlátozódik, azaz helyi jelenség! Éppen úgy, mint a gravitáció! Annak feltételezése tehát, hogy a világtérben a mágneses tér mindenütt jelen van, minden valós alapot nélkülöz, és a jelenség félreértésén alapul.
A másik tapasztalat ezzel az eszközzel az, hogy a tér alakja 3D-ben is valóban olyan, mint amilyennek a fólia síkban mutatja. A semleges zóna felett az eszközünk kis mágnese a két pólus irányát mutatva a mágnes testével párhuzamosan áll! Innen bármely irányba elmozdítva, a közelebbi pólus felé eső vége lehajlik (inklináció), a mágneses erővonalak irányát követve.
Eddig egy aktív mágneses eszközzel tapogattuk le a tér alakját, tehát most próbálkozzunk meg egy passzív ferromágneses eszközzel, ami nem más, mint egy vékony, hajlékony vas drótszál. A hajlékonyság lényeges, mert másként nem fogjuk látni a tér letapogatása során az erővonalak irányát, amit a drótszál elhajlása jelez. Ezért érdemes olyan vékony és olyan hosszú szálat választani (vagy a hosszú szálat megfelelő helyen fogni), amely nagy érzékenységet tesz lehetővé.
Az ezzel az eszközzel végzett térletapogatás a következőket mutatja: 1) Ha a szál végét közelítjük a mágnes egyenlítőjéhez, akkor azt tapasztaljuk, hogy nem tudjuk vele elérni a mágnest, mert a mágneses tér határát elérve a szál vagy az egyik, vagy a másik pólus felé el fog hajlani, akármilyen pontosan is igyekszünk azt a két zóna között tartani. 2) A kezünkkel érezni is fogjuk, hogy a mágnes szó szerint eltaszítja ezen a helyen a vasat, és ezzel belelöki az egyik pólus felé tartó térbe. Más esetben olyan tapasztalat nem létezik, hogy a mágnes a vasat eltaszítsa, mindig csak vonzza, és bármely pontján vonzza! 3) Ha ekkor a szálat rövidre fogjuk, hogy az ujjunk közül csak kb. 1 cm álljon ki, azaz ne tudjon elhajolni, azt tapasztaljuk, hogy ekkor már le tudjuk nyomni a szál végét a mágnes felszínéig, ahol az oda is tapad. De még ekkor is érezzük, hogy utána a közelebbi pólus felé igyekezne. Ez azt jelzi, hogy a tér a test mágneses egyenlítőjének két oldalán különböző irányú a tér határától végig a mágnes felszínéig.
Az eddigiekből megint levonhatunk egy eddig nem levont következtetést. Azt, hogy a mágnesség térirányító hatás. Azaz, a mágnes terébe bekerült, reagálni képes testek mozgását (ideértjük a részecskéket is, amelyek parányi szilárd testek) a mágneses tér eltéríti, irányítja. Ezt az összefüggést ismerjük abból, hogy az elektroncsöves TV elektronáramát ezért vagyunk képesek irányítani. A különbség csak annyi, hogy ott elektromos árammal keltett, és azzal fenntartott ideiglenes, és más formájú térrel rendelkező mágnességről van szó, ami jelentősen eltér az állandó mágnesektől, amint azt látni fogjuk.
Következőként bemutatunk néhány olyan kísérletet, amely azt mutatja meg, hogy a mágnessel valóban nem forog együtt a mágneses tér. Ennek egyik első példája a fentebb látott video a szupravezetésről. Láthattuk ugyanis, hogy a mágnes tere összekapcsolta a mágnest a lehűtött testtel, azaz abba oly módon „záródott” bele a tér, hogy a két testet távolságtartó módon összekötötte. De vajon iránytartó módon is összekötötte-e őket?
Az jól látszik, hogy a lehűtött testbe iránytartó módon rögzült a tér, míg a mágnesben nem. Ezt abból láthatjuk, hogy a mágnes szabadon (és fékeződéstől mentesen!) forog a test feletti térben, ugyanakkor a lehűtött test nem fordul el vele együtt. Ha ugyanis a tér is forogna, akkor annak a lehűtött testet is forgatnia kellene a mágnessel együtt, vagy ha ez lehetetlen a súrlódás miatt, akkor erősen fékeznie kellene a mágnes forgását is, vagy teljesen lehetetlenné tenni. De semmi ilyesmit nem látunk.
A következő ilyen kísérletekhez a már ismert fóliát használjuk, valamint kontroll eszközként két plexi lap közé beszórt, szabadon mozogni képes vasreszeléket használunk.
Mindkét eszközzel azt tapasztaljuk, hogy sem a rúdmágnes pólusai, sem a gyűrűmágnes pólusai, ha a mágneses tengely mentén forgatjuk, nem viszik magukkal a teret, és azzal a vasreszeléket. Azonban, ha a mágnest oldalt fordítjuk, és az egyenlítőjén átmenő tengely mentén forgatjuk meg, akkor azt látjuk, hogy a tér elfordul a mágnessel együtt, és magával viszi a vasreszeléket is, amely így ezt jól mutatja. Erről az is jól leolvasható, hogy a mágneses tér erővonalai a forgatástól nem torzulnak el, nem „maradnak le” a vasreszelékben, hanem a vasreszelék marad le, ha nem tudja követni a tér fordulását.
Ez utóbbi jelenség különös figyelmet érdemel, mert egy tudományos félreértést és annak minden következményét küszöböli ki a felismerése. Nevezetesen azt, hogy a forgó test mágneses tere „felcsavarodik” és más módon is torzulni képes. Ez a jelenség egyszerűen nem létezik. Nem több mint elméleti spekuláció, amit soha nem ellenőriztek le a gyakorlatban. Pedig éppen ezen az alapon feltételezik, hogy a Nap mágneses tere felcsavarodik, a felszínéhez közel pedig torzul, és éppen ez hozná létre a napfoltoknak nevezett jelenségek megfigyelt „működését”. Nos, ez a magyarázat nem valós! Tessék másikat találni helyette! (Mellékesen megjegyezzük, hogy a napfoltok tipikusan a forró folyadékok felszínén tapasztalható hőáramlási és főként a hűlési jelenségek jellegzetességeit mutatják, és leginkább a felfúvódó, majd elpattanó buborékokra hasonlítanak, mint bármi másra.)
Kimondhatjuk tehát a következtetést: A mágneses tér a mágneses test forgásától nem marad le, nem torzul el, és nem is csavarodik fel!
A továbbiakban azt nézzük meg, hogy milyen esetekben forog együtt a mágneses testtel a benne és körülötte kialakult mágneses tér, ha a mágneses tengely körüli a forgás. Ehhez megint a fóliát és a vasreszeléket használjuk. Ehhez azonban néhány gyakorlati ismeret is kell az állandó mágnesek egymással való viselkedéséről. A következő jelenségek csak azok számára ismerősek, akik eleget „játszottak” sok kis állandó mágnes összerakosgatásával, ezért érdemes ezeken előbb végigmenni.
1) Az közismert, hogy ha több rúdmágnest engedünk hosszában összetapadni, akkor az így létrejött mágnes erősebb lesz, mint egy rúd volt. Az viszont nem annyira ismert, hogy ha ezt a rudat összehajtogatjuk, hogy a mágnesek egymás oldalához tapadva szalagot alkossanak, akkor az erősségük lecsökken.
2) Az sem nagyon ismert, hogy az így összehajtogatott mágnesekből egy gyűrűt formálhatunk, de csak akkor, ha páros számú mágnesből áll. Másként, páratlan számú mágnessel nem fog sikerülni, az egész szét fog ugrani, és újra egyenes rúddá áll össze.
3) Az még kevésbé ismert, hogy páratlan számú rúdból mégis alkothatunk gyűrűt, ha elegendő számú mágnesünk van (az előbbi gyűrűhöz szükséges szám többszöröse), és a szalag két végét egy fél fordulattal illesztjük össze. Ekkor egy mágnesekből álló Möbius szalagot (egyfelületű, egyélű végtelenített szalagot) hozunk létre, amelynek a mágneses tere különös jelenségeket mutat, de mindenesetre annyira legyengül, hogy már szinte nem is észlelhető.
Ilen a tere pólusirányból (fent), és ilyen oldalról
Teszi mindezt annak ellenére, hogy a képen látható szalag olyan, 8mm hosszú és 3mm átmérőjű hengeres mágnesekből áll, amelyek egyenként 30 dekánál nehezebb vas testeket képesek megtartani még úgy is, hogy azzal egyetlen ponton érintkeznek!
4) A Möbius mágnesszalaghoz azért van szükség ilyen sok mágnesre, mert a terükkel párhuzamosan illeszkedő mágnesek csak igen kis elhajlást engednek meg anélkül, hogy a terük szétválna, és az egész szétugrana. Ez sem annyira közismert megfigyelés. De ha csak két mágnest tartunk így a kezünkben, még ha azok csak egy ponton érintkeznek is, ha el akarjuk csavarni őket a párhuzamostól, akkor erős ellenállást mutatnak a csavaró erővel szemben. Azaz a terük összekapcsolódott oly módon, hogy a külső terük egymás belsejébe záródva fut. Láthatólag ugyanolyan módon kapcsolódott össze a két mágnes a terükön keresztül, mint ahogyan a videón szereplő mágnes és a lehűtéssel passzivált test.
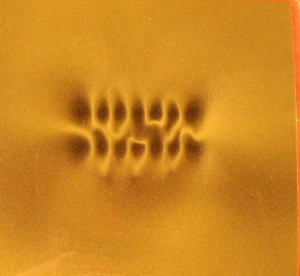
Most már elég ismeretünk van ahhoz, hogy tovább folytassuk a tér viselkedésének bemutatását. Az első képen a fentebb leírt, rudakból hajtogatott mágnesgyűrű egyik pólusának a terét látjuk a fólián.
A képen semmi különös nem látható, csak az egyes mágnesek pólusainak tere és a csatlakozások semleges zónája. A valódi látni és megfigyelni való akkor jön létre, amikor ezt az alakzatot az indikátor eszköz alatt elkezdjük elforgatni.
Azt tapasztaljuk ugyanis, hogy ezzel a mágnessel együtt forog a mágneses tere, noha látszólag a mágneses tengelye körül fordítottuk el. Ez valójában egy látszat csupán, és egy, a matefizikában nagyon mélyen gyökerező félreértés, amit muszáj tisztázni! A gyűrűnek ugyanis nincs, és nem is lehet tengelye! Ha van, akkor nem gyűrű, hanem korong! A mágnesgyűrűnek pedig végképp nincs, amint azt alább majd be is mutatjuk. Az okozati összefüggés itt ugyanis éppen fordított: nem a tengelye körül forgattuk meg a gyűrűt, hanem a gyűrűt forgattuk meg, amely által látszólag, a képzeletünkben keletkezett egy kép, mintha a gyűrű közepén lenne egy olyan pont, amely körül az forog. Azaz a tengely csak képzetes és virtuális a gyűrű esetében. A mágnesgyűrű esetében ez a kép még hamisabb. Ugyanis ennek a mágnesgyűrűnek éppen annyi valódi mágneses tengelye van, ahány mágnesből áll, de nincs egyetlen közös tengelye sem, hiszen ott nincsen mágnes, és láttuk, hogy mágneses tengely csak a mágnes belsejében, annak leghosszabb átlója mentén alakul ki. Itt pedig ilyen nincs!
Most pedig következik egy még ennél is meglepőbb tapasztalat. Egyetlen, látszólag homogén gyűrűben is lehetséges több mágnes mágneses terét létrehozni ahhoz hasonlóan, mint ahogy mi a gyűrűt összeraktuk. Csak éppen porkohászati úton. Itt a képe:
Látszólag egy hangszóró gyűrűmágneséről van szó, de ez nem így van. Ez egy CD lejátszó fedelének leszorító gyűrűje alól kiszerelt mágnes. A hangszóró mágneseknek nincsenek ilyen szekvenciái. Láthatjuk, hogy ennek a mágnesnek a terét hat valódi mágneses szegmens alkotja, noha anyaga homogén lehet. Ilyet csak mesterségesen lehet létrehozni. És az érdekesség: ezt megforgatva, ezzel a gyűrűvel is vele fordul a mágneses tere.
De nem csak a különlegessége miatt mutattuk meg ezt a gyűrűt. Meg akarjuk ugyanis mutatni, hogy minden mágnesnek vannak ilyen szegmensei, szeletei, amelyek mintha különálló mágnesek lennének, DE CSAKIS A GYŰRŰ SEMLEGES EGYENLÍTŐJÉN észlelhetők. Nem úgy, mint a fenti mágnesnél a pólusoldalakon. És ennek a jelenségnek rendkívül messze vezető következményei vannak a Föld mágneses tere megértésében, amit a következő írásban fogunk részletesen kifejteni!
A jelenség bemutatásához kell egy nagyméretű gyűrűmágnes, egy nagyméretű korong mágnes, valamint egy-egy kisméretű gyűrű és korong-mágnes, továbbá egy acélgolyó.
A vizsgálat meglehetősen egyszerű. Elsőként fogjuk a nagy gyűrűmágnest, és a kerületére tegyük rá a kis gyűrűmágnest. Meglátjuk, hogy a polaritás nem mindegy ebben az esetben sem. Csak egyetlen irányba állva marad meg a kerületen, a semleges zónán egyensúlyozva. Ekkor kezdjük el előbb nagyobb, majd kisebb erővel körbe lökdösni a kis mágnest a kerületen. Elég nagy erővel meglökve, akár több fordulat után áll meg valahol. Egy idő után azt vesszük észre, hogy egyenlő erővel meglökve mindig ugyanazon a ponton áll meg. Jelöljük meg ezt a pontot a gyűrű lapján, majd folytassuk a játékot. Azt is észre fogjuk venni, hogy egyes helyeken úgy áll meg a kis mágnes, mintha ott valami hirtelen megállította volna. Ha elég sokáig folytatjuk, és minden ilyen megállás helyét megjelöljük a nagy gyűrű lapján, akkor végül azt találjuk, hogy a gyűrű kerületén tíz (10) ilyen hely van. De azt is láthatjuk, hogy közöttük a távolság nem mindenütt egyforma.
A következőkben, ellenőrzésképpen, ismételjük meg a kis korong-mágnessel és az acélgolyóval is a kísérletet. Azt fogjuk tapasztalni, hogy ugyanezeken a helyeken állnak meg ezek is (esetleg a korong-mágnesnél egy kis eltéréssel). Különösen a nem mágneses acélgolyónál vehetjük észre, hogy a kerületen egy hullámvonalban szalad végig, hol az egyik, hol a másik laphoz közelebb, mintha a gyűrű több, ellentétes pólusaikkal összeillesztett mágnesből állna, és a golyó mintha az ezek által kijelölt hullámzó vonalat követné.
A következőkben járjunk el ugyanígy a korong-mágnes esetében. Ennél azt figyelhetjük meg, hogy csak négy olyan helye van, ahol a körbelökdösött kisebb testek hirtelen, látható erőhatás hatására, feszesen rezegve állnak meg. Ezeket a helyeket nevezzük a rendszerlogikában a mágneses tér szegmens határainak, amelyből a rúdmágnesnek négy, a gyűrűmágnesnek tíz van.
A magyarázat erre a jelenségre is roppant egyszerű a fentebb látottak fényében. A nagyobb kerületű mágnesek, még akkor is, ha kényszerített a mágnesség bennük, kisebb virtuális mágnesek alakulnak ki, ha az átmérő akkora, hogy egyetlen mágnes gyenge tere már nem képes átfogni. Ide kívánkozik az a gyakorlati tapasztalat, hogy azokat a testeket lehet a legjobban mágnesezni, azok lesznek a legerősebb mágnesek, és azok veszítik el legkevésbé mágnességüket, amelyek hosszúság – átmérő aránya kisebb, mint 4:1. Azaz, a hosszúságuk jóval meghaladja az átmérőjüket, de a négyszeresnél nem jobban. (A túlságosan hosszú és igen kis átmérőjű mágnesek jelenségeivel majd a csúcshatás tárgyalásánál fogunk találkozni.)
Az előbb vizsgált gyűrű és korong nem felel meg ezeknek az arányoknak, ezért bennük a mágnesség „felosztódik” kisebb, virtuális mágnesekre. A korongnál, amely egytestnek van valódi forgás és mágneses tengelye, mert a közepe nem üres, négy ilyen virtuális mágnesre osztódik a tér, majd ez egyesül egyetlen térré a tengely mentén. Ezért nem lehet a jelenséget észlelni máshol, csak a kerületen. A gyűrűnél, amelynek egytestként nem lehet sem mágneses, sem forgástengelye, a gyűrű anyagában kénytelen eloszlani a mágneses tér virtuális mágnesekre, és a tér az üres közép virtuális mágneses tengelyénél egyesül. Ezért ennek is csak a kerületén lehet észlelni a kvázi szegmenseket.
Ha most visszaemlékszünk a különleges gyűrűmágnes terének képére, akkor a semleges zónák határához képzelhetjük a virtuális szegmensek határát. Itt felmerülhet a kérdés: csak képzelhetjük, vagy van is? Az előbbi kísérlet szerint van is, de van rá még egy tudományos bizonyítékunk is. A Föld mágneses terét évekig megfigyelő űrszonda csoport észlelt ilyen mágneses anomáliákat magasan a Föld mágneses terében, amelyeket kapuknak neveztek el. Tehát megtalálták már a jelenséget a Föld mágneses terében is, csak éppen nem ismerték fel az okát. (Ez egy jó alkalom arra, hogy újabb tudományos tündérmesét találjanak ki, és fogadjanak el közmegegyezéssel.)
De ha már a Földnél tartunk, akkor bemutatunk egy másik érdekességet, amely nagy valószínűséggel a Föld mágneses teréhez, annak változásához és a nemrégiben felfedezett mágneses kapukhoz is köthető.
Elsőre talán nagyon ezoterikusan hangzik, de vannak olyan monolitikus építmények a Föld felszínén, amelyek elhelyezkedése nagy szabályosságot mutat. És éppen olyat, amilyet az imént fedeztünk fel a gyűrűmágnes egyenlítőjén. Ráadásul még az eloszlásbeli különbségek is nagyon hasonlóak.
Ennek bemutatásához a Google Earth program távolságmérő eszközét, és annak mentési lehetőségét használtuk fel a megjelölt monolitikus építmények közötti vonalak meghúzására. Ezt bárki megismételheti, és maga is láthatja, hogy nem tévedtünk.
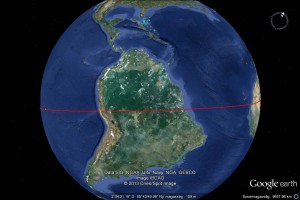
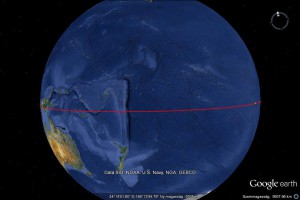
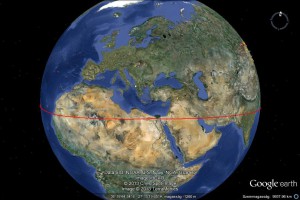
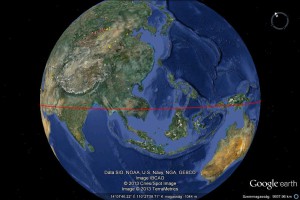
A következő pontokat kötöttük össze ebben a sorrendben: Az egyiptomi nagy piramisoktól nyugat felé húztunk egy vonalat a Szenegál folyó régi torkolatvidékéig, ahol ismeretlen eredetű hengeres kőoszlopok csoportjai állnak. Onnan az Atlanti óceánon keresztül húztunk egy vonalat az Amazonas torkolatánál fekvő szigetig, ahol hatalmas, földalatti monolitikus építményeket találtak. Onnan tovább húztuk a vonalat Machu Picchu monolit városáig. Onnan továbbhúztuk a vonalat a Nazca vonalrajzok felett a Húsvét szigetig, ahol a monolit kőszobrok találhatók. Ezután az egyiptomi nagy piramisoktól keletre húztuk a vonalat a Tigris és az Eufrátesz torkolata felett Mohenjodaro ősi romvárosáig, majd onnan tovább a kambodzsai Angkorig. Angkortól tovább húztuk a vonalat Új Guinea északi csücskén található monolit romokig. Végül Új Guineát a Csendes óceánon keresztül egyetlen vonallal összekötöttük a Húsvét szigettel. Eközben (épp a megfelelő távolságban) kereszteztünk egy nagy É-D irányú tengeralatti törésvonalat, ahol azonban nincs szárazföld. Ezeket a helyeket így összekötve, végül egy tökéletes legnagyobb kört rajzoltunk a Föld felszínére, egy egyenlítőt!
A lényege az egésznek az, hogy az összekötő vonalak egy egyenlítői kört adnak ki! Ettől a körtől egyenlő távolságokat lemérve Észak és Dél felé, egy tengely két végét találhatjuk meg a Föld felszínén, amelynek északi pólusa az Alaszka nyugati partjainál fekvő Knight sziget közelében van. Tehát akár a Föld valamikori mágneses tengelyét és valamikori mágneses egyenlítőjét is jelezheti ez a tíz hely.
Következzenek a Google Earth segítségével a fentebb elmondottakról készült képek. Ezek magukért beszélnek.
Folytatása következik.


 Téma:
Téma:  Címkék:
Címkék: