Introduction to the method of morphology modelling
The morphology modelling is a practical method that makes accessible the invisible and manageable the inaccessible. Although this might sound unbelievable but that is literally the case because it can be proved in practice. Whoever has seen the small scale model of an object or a house actually saw theresult of true to life modelling. That is what morphology modelling does in the other direction, produces the large scale models of atoms and molecules by using the rules and connections of morphologic compatibility. In Mother Nature there are no misfits or square pegs in round holes. Everything is compatible or if not, than nonexistent. This recognition makes morphology and modelling a true mirror to reality.
Up scale modelling is made possible by the same fact, which makes possible small scale modelling: solid material bodies (solids) have unalterable properties. One of them is that solids fill in a certain piece of the 3D space, that is, they have volume. The other is, they have density. The two together add up to mass in the Newtonian sense. But there is a third, usually forgotten property of solids: they have some shape even if we are not aware of this shape. During modelling this shape, the true to life form is to be found.
The only thing to do in modelling is to find that form and find a property unchanged along which we can up-scale the invisibly small objects like elementary particles. This property is the geometric form of their planar or other surfaces that can be measured, and the correct angles of them can be made visible by other scientific methods.
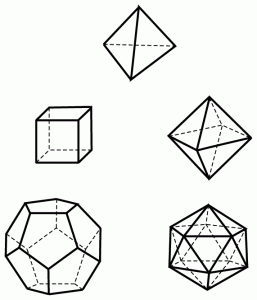
It is a known fact that surfaces of solids can be planar and in 3D space objects have a spatial form which is made up of surfaces. Planar and spatial forms can be regular even symmetrical or irregular. (Or at least so they seem.) To illustrate this let us see the Platonic solids.
Platonic solids. Source: Wikipedia
| Tetrahedron | Hexahedron | Octahedron | Dodecahedron | Icosahedrons |
Though it is not obvious at first sight one of the Platonic solids has more to it than meets the eye. It has no diagonals going through between two points within the body, and has no parallel surfaces like other solids do. This solid is the tetrahedron. Its properties are going to be important when reactions to external impacts will be modelled for these are dominantly determined by the form of planar surfaces and their relations (angles) to each other. Based on these special properties tetrahedron will be one of the basic building stones of nuclear and molecular modelling as it is in Mother Nature.
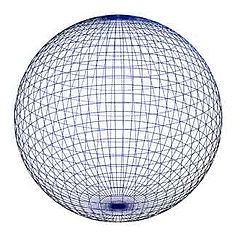
But we can notice too, although it can be found everywhere in nature, the sphere is not among the Platonic solids presumably because it is not bordered by regular planes. Since in morphology modelling it is not a key factor, sphere – as a geometric form – will be another one of our basic building stones.
Sphere. Source: Wikipedia
Though it is a well known form in daily life let us see it as if for the first time and contemplate on the question: What makes a sphere a sphere? The everyday answer to this would be: All surface points of it are at an equal distance from a central point imagined. The answer might be correct, but not in morphology. This kind of property gives us nothing for no one can see or find the central point and measure the distance. In morphology we need a more obvious one. For morphology and for modelling, too, sphere is a surface whose bend is equal between any two points in all directions. This is how the human eye and other senses recognise a sphere. This is what is evident at the first sight. Seemingly, this answer (specification) gives us nothing more than the previous one but this is not the case. Behind this specification there lies another: Sphere is the form of a body which has no singular place on its entire surface. That is, every point on its surface is equal to any other. And this is the property, which is the most important in morphology for sphere is the form that cannot be fit to any other sphere or any other solid at more than one single point.
With this we have arrived to the first cornerstone of morphology and modelling: connectivity and compatibility. What is connectivity and compatibility in morphology modelling? It is the property of solids that they can be connected by fitting their planes together if their form is compatible. This way solids can be bonded together to form a new single body. In case of two spheres this property does not exist. No matter how hard we try they will not fit together only touch each other at a single surface point. Consequently they are not compatible. But morphology figures it differently. More than two spheres are compatible but in a different and peculiar way. That is why connectivity and compatibility forms the basis of morphology modelling.
In morphology modelling the sphere is a regular solid. So we can use the sphere to show an important fact to be considered in modelling. When we fit two solids together, especially spheres touching only at one single point it is important to know whether they are massive bodies or empty shells of a body. It is important to know to determine whether the bonding force will be strong enough to keep them together, or the masses are too big for the force applied. Massive solids need strong force especially when their surfaces touch but one single point. On the other hand shell bodies need less force. That is why in morphology modelling we make distinction between massive and shell solids. Shell solids are only surfaces with no mass surrounding an empty space.
Illustration: Cross section of a layer covered shell sphere and a solid sphere.
The illustration shows that the two dimensional cross section of a sphere is a circle, but the cross section of a shell sphere is a ring even if we do not regard any thickness to the surface layer. Later on the coloured circle shall mean a sphere and the ring shall mean a shell sphere.
The most important factor of connectivity and compatibility is the surface. Surface also seems to be a well known concept but in fact it is not. Usually we do not think about it as a bordering layer dividing the interior of a body from the external environment. Therefore in morphology modelling the surface is called border. Also it is a two-way medium mediating external effects towards the interior of the body, or vica-versa, or not at all, which is another important property of borders. Furthermore, with its form, it makes possible the connection between two solids, or not. These properties of it can be determined in an exact way by modelling.
Besides their geometric form the smoothness or roughness of border surfaces make an important role in compatibility. In general, it is easy to see: the bigger the touching (connecting) surface the stronger the force – no matter how strong it is – between the two particles. It also means that the bigger the touching surface and the connecting force, the bigger force must be applied to separate them. This is a fact known from everyday experience. Smooth surfaces are usually more compatible than rough ones for the touching surface is bigger, the number of touching points are bigger.
But smoothness is a relative concept, which must be specified (defined) in morphology, too. Since all material body (solid) consists of smaller parts and smaller parts (particles) are also built of still smaller parts we can – without even knowing them – continue going down this line until we arrive at points so small they cannot be measured. Therefore, in morphology modelling surfaces are regarded as number of touching points when strength of a connection is to be determined.
This way the size of the touching border surfaces and the relative strength of the bonding force can be determined by the number of touching points. This is a particularly important factor in morphology modelling because on this scale we never deal with perfectly smooth surfaces. That is why the number of touching points is so important. Based on this number and on the mass of bonding bodies we can determine whether the connected solids modelled would stick together to form another stable single solid.
But the number of touching points depends on the form of the surface. Plane surfaces would bond with all their surface points. But this is only an ideal case, which almost never occurs. Ideal plane surfaces are very rare in Nature. Surfaces are usually not planar and bond together at fewer points than the ideal. Therefore, in morphology modelling, solids can be bordered by ideal plane surfaces in macro-view and by non planar surfaces in micro-view at the same time. Let us see it on a model.
Illustration: Tetrahedron constructed of equal sized spheres.
The illustration shows a tetrahedron constructed of equal sized close packed spheres. The bordering surfaces of the tetrahedron are – in macro-view – plane surfaces but for compatibility (in micro-view) they are rough surfaces.
With this we have arrived at the second cornerstone of morphology modelling, to those properties of space among which solids are to be connected to each other during modelling. In morphology space is the part of space filled in by the solid modelled. Otherwise space is considered empty in morphology. (Empty here means: having no form or shape, therefore contains no matter.) Though it is considered empty in morphology space still have properties for it is still considered a medium. In this respect space can mediate effects and when it does so it is called directed space. When there is no effect present in space it is free from direction (free space).
Let us see what space-direction in practice is. Since in morphology models are created to be true to life images therefore effects in real life must be taken into consideration during modelling for they modify morphologic compatibility in real life. What does that mean in practice?
In real life all matter is affected by effects. One of them is gravity, which affects all material objects a different way. Another one of effects is magnetism, which divides material bodies into two categories in morphology modelling: to those affected directly by ferromagnetic effect and to those that are affected (or not at all) by other forms of magnetic effects. A similar effect is the interaction of electric charges, which in morphology is also a dividing factor: an effect resulting in keeping distance between objects and an effect bonding them together. In short, the space in which similar effects are present is called directed space in morphology. In morphology modelling it does not matter whether they are strong or weak, what size of the space is filled with them or how far they can reach. Simply their existence and presence is what counts for they can indicate whether the particle modelled is a true model or not. The models we create in morphology modelling are constructed in gravitational space on Earth therefore effects of gravity must always be counted in.
Let us see an example. On Earth the surface of water is always at right angles (perpendicular) to the direction of gravity. That is what we call horizontal which is a name of this phenomenon on its own right because it is a reliably unchanging fact in real life on Earth. Therefore this direction can be used to compare other directions. At the same time water on the board of a spaceship in outer space does not show this property. In no gravity circumstances water always forms a sphere when it is not in a container bordering it. It may seem that no effect is present in outer space, that is, outer space is a non-directional space. So it seems, but in morphology we figure it differently. When a form reliably takes shape in Nature there must be a reason (an effect) behind it. That is when we can use the method of up-scaling not only in the physical modelling of a body but modelling effects, too, via the shape of that body.
Let us have a look at the phenomenon through the eye of morphology modelling. Seemingly we have two different shapes of water surface, planar on Earth, spherical in deep space. Up scaling the deep space model we can easily come to a conclusion that the two are identical. Since Earth is a sphere, water on its surface is the surface of a sphere but when we only see a small part of it we think of it as planar. The up scaled model also makes it possible for us to identify the effect responsible for this shape. This is gravity in both cases. But this also means that gravity is a directing effect of space which comes from and equal in all direction. That is how we consider gravity in morphology modelling and we always count on it in the construction of models. Otherwise, considering compatibility, the all-directional space and the non-directional space would be equal in morphology modelling.
The working hypothesis of morphology modelling is that all matter consists of smaller material particles. For morphologic purposes even the smallest, not yet discovered particle is a material body that consists of smaller particles with specific shape, density and volume. In modelling there is but one exception: the undividable atom as the original concept theorises the smallest particle in Nature. Since in science atom means the particle of chemical elements in morphology modelling the smallest particle is called primary atom. In modelling primary atom is regarded a sphere with no measurable properties. (The properties of matter are all there, but they are not measurable!)
With this we have arrived at the third cornerstone of morphology modelling, which consists of several hypothetic – but proven in practice – statements. These statements are connected to the basic method of modelling, the up-scaling and open the gate of a new system. These are the following: If and when the shape of one of the building particles of matter is postulated a sphere, this has the inescapable consequence in morphology: A larger sphere can be built of equal sized spheres only when the number of spheres reaches a certain magnitude. This magnitude can be specified. This proportion between magnitudes following each other remains the same.
In other words: If the shape of any of the particles at any magnitude is postulated a sphere it must be understood that there is no way that the shape of the particle constructed of these spheres would be a sphere. Also, there is but one way of constructing other shapes or a sphere out of equal sized spheres. Morphology modelling shows that all matter consists of particles. The particles form an ascending periodic series where the first particle of the series is a sphere and the second is a tetrahedron of four close packed spheres. This particle is called tetra-particle in general.
In morphology modelling the passive particle of the primary atom, the neutrino, the electrino and the neutron and their active counterparts are considered as being spherical. In modelling the particles that are active in bonding are called active, and those having no active role in bonding are called passive particles.
(In modelling electrino is the name of the hypothetic spherical particle, which is ¼ of the electron which is a tetra-particle in morphology modelling.)
During nuclear and molecular modelling the neutron-proton passive-active particle pair shall be used since they are the primary particles in the fourth magnitude of the particle series.
Illustration: tetra-particle constructed of four equal sized spheres in slose packed structure.
The following particles shall be used in modelling since they are building stones of matter on their own right in this structure and shape.
Illustration: pairs, plain triples, tetra-particle, incomplete tetrahedron base particle.
The last particle shall be a panel (module) in modelling. We shall come to this particle during practical modelling and the special properties of it shall be analysed in due course.
The aim of morphology modelling
The aim of morphology modelling is to figure out shapes, forms, structures, bonding used by Nature by modelling.
The basic rules of morphology modelling
Rules:
1. A structure constructed of equal sized spheres in directed space shall pack in closest packed structure. No other packing is valid in modelling.
Illustration: closest packed structure of equal sized spheres (existing structure of one and two layers)
Illustration: 1-2-3 layer nonexistent structures
2. The direction of all movement is the direction of the least resistance.
3. Rule of decreasing bonding force. The bigger the particle, the smaller the relative bonding forces.
4. Connection between bonding force, bonding surfaces and mass. Bigger mass needs stronger bonding force. Smaller surfaces need stronger bonding force.
5. No bonding is possible without compatible bonding surfaces.
6. Without external effect matter keeps its original shape.
7. Always the biggest possible building block must be used in modelling until proven inadequate. Incomplete shapes are entities on their own right in Nature so they must be in modelling.
8. Connection of changing forms. When a particle has reached its perfect form a new, incomplete form shall be formulated next.
9. The existence of structural and formal allotropes.
10. The solids in modelling are regarded single bodies.
Possible bonds in morphology modelling
Types of bonding:
1) one sphere – one sphere bond (free bond)
2) one sphere – three spheres bond (rotational bond)
3) three spheres – three spheres bond (small plane bond)
4) three spheres – five spheres bond (large plane bond)
5) four spheres – four spheres bond (fours bond)
6) large planar surface bond.
They all can all be supported by smaller particles and reinforced by a space directing force or both.
Relative strength of bonds in morphology modelling
The strength of bonds between active-active particles is considered 1 (one). The strength of bonds between active-passive particles is considered 1/2 (half). The strength of bonds between passive-passive particles is considered 1/4 (a quarter).
Methodological principles of applied morphology modelling
True to life models must be found via the comparison of model properties with natural properties of particle modelled. All other variations must be eliminated.


 Posted in
Posted in  Tags:
Tags: